tsetse

Welcome!

This is a collection of various variants on the card game Set. They are all original ideas developed by members of ET, inspired by other variants such as Proset and Nonabelian Set.

An average of 1 physical deck exists in the universe for each of these variants. If you want to try playing with them, come visit ET. I promise it's worth it.

This site provides online multiplayer implementations -- play with your friends in real time!

How to play
  C53T
  FO1D
  FOLD
  OCTA
  A5SET
  S3CT
  C3C3
Credits / About
Photo gallery

How to play

In general, you will see a collection of cards on the board, and your goal is to find ones that form a "set". The rules for what a "set" is are different for each variant; all of them are explained below. When you've found a set, you can click or tap the cards to select them.

To submit a set, press the checkmark button in the bottom right. You can also press Enter, if you're playing on a computer. In some set variants, all cards have the same number of sets, in which case your sets will be submitted automatically.

In the sidebar, you will find scores (which count how many cards each player has taken) as well as preferences for each variant (e.g. how many cards to display per row).

Note that the difficulty levels listed here are relative. Even the ones labelled "easy" are quite difficult.

C53T

difficulty: very hard

cards: 125 (deal 12)

pronounced "see-set"

Here is an example of a set in C53T:

A set consists of exactly 5 cards such that for each pentagon (light, medium, and dark), the 5 pentagons overlaid on top of each other form a pattern with a line of reflectional symmetry. In the above example, the light pentagon is symmetric across the red line, the medium pentagon is symmetric across the orange line, and the dark pentagon is symmetric across all 5 lines.

Here is a sketch of all the ways for the lines on a set of 5 cards to be symmetric, up to rotation:

The underlying mathematical object is the natural torsor for (C₅)³, whence the name; here C₅ denotes the cyclic group of order 5. The rule can equivalently be stated as "pick 5 cards that add to the identity".

FO1D

difficulty: medium

cards: 70 (deal 12)

pronounced "foyd-set"

Here is an example of a set in FO1D:

A set is a collection of cards with non-overlapping creases, which form a flat-foldable crease pattern when overlaid. Red lines represent mountain creases, and blue lines represent valley creases.

To figure this out in practice, it is enough to know the following fact: if a single-vertex crease pattern is flat-foldable, you can always fold it by making a series of crimps (and you can never ruin it by making a "wrong" crimp).

To make a crimp, find a mountain crease and a valley crease with no creases in between, where the distance between the two creases is at most as large as the distance to any other creases.

Then fold both creases. This effectively deletes the paper between the two creases, as well as the same amount of paper on one side.

If your cards are a set, you will be able to repeatedly do this until there are just 2 creases left, at which point they will form a single line and can be folded straight through.

For a proof of this fact, see lecture 2 of Geometric Folding Algorithms, a class taught by Erik Demaine at MIT that inspired this variant.

Here are some other useful lemmas for finding sets in this variant:

A set must contain either 3 or 5 cards.
A set must satisfy the Kawasaki condition: the sum of alternating angles is 180°.
The number of mountain creases and the number of valley creases in a set must differ by exactly 2.

FOLD

difficulty: hard

cards: 98 (deal 12)

pronounced "fold-set"

Here is an example of a set in FOLD:

FOLD is very similar to FO1D; you should read those rules if you haven't already. The only difference is that FOLD cards have two vertices instead of one, and they are connected by an unassigned crease present on every card. A collection of a cards is a set if it is flat-foldable for either assignment of the center crease (but both vertices have to agree).

The specific layout of creases in FOLD -- that is, six equally spaced creases around each vertex -- lends itself to a set of rules equivalent to flat-foldability, but making no reference to folding. You may find that you can find sets faster using this characterization instead of making mental crimps. In particular, all sets contain either 3 or 5 cards. For 3-card sets:

A set must contain an even number of two-color cards (i.e. cards with both red and blue). This guarantees the existence of an assignment for the center crease that satisfies both vertices, and in fact there is a unique one: each vertex must have either 3 red and 1 blue or 3 blue and 1 red. So in the above example, the center crease should be red.
The pattern of creases around each vertex must form a "chicken foot" -- i.e. three equally spaced creases plus an extra crease.
The chicken foot can appear in any rotation; in the above example, the top foot has its heel pointing northeast, and the bottom foot has its heel pointing south. (This requirement is equivalent to the Kawasaki condition.)
As mentioned, each vertex must have 3 of one color and 1 of the other. The "heel" of the foot cannot be the odd one out. In the above example, both vertices have 3 red and 1 blue, so the heels have to be red.

For 5-card sets, there is only one requirement:

The number of mountain creases and the number of valley creases around each vertex must differ by exactly 2. Again, this means that there must be an even number of two-color cards, but that is no longer sufficient to guarantee that this requirement holds.

You may note that all of the conditions above only talk about each vertex separately; indeed, the only way the two vertices interact is by requiring that they agree on the assignment of the center crease.

OCTA

difficulty: easy

cards: 48 (deal 9)

pronounced "octaset"

Here is an example of a set in OCTA:

OCTA is all about how to get from one card to another. A set is three cards such that the way to go from the first card to the second card is the same as the way to go from the second card to the third card.

There are four different ways to think about going from one card to another, and they are all equivalent (!).

The bottom half of each card depicts a cube where some faces are "hollow". Opposite faces of the cube are the same color but different hollowness, so you can always tell what all the faces are even though you can't see 3 of them.

The transformation from one card to another is an isometry of the cube; i.e. a rotation, reflection, or combination of both. In the above example, the rotation is 90° clockwise around the line that goes through the center of the green face:

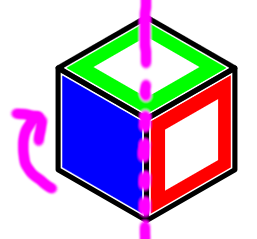
Note that from the first card to the second card, the hollow red face rotates clockwise, and the hollow blue face (which was previously hidden) rotates into view. Similarly, from the second card to the third card, the hollow blue face rotates clockwise, and the solid red face rotates into view.
The top half of each card depicts an octahedron. Opposite faces are again the same color. Furthermore, each octahedron has a swirl on top representing the handedness of the octahedron: since opposite faces are indistinguishable, the swirl is necessary to tell you whether the octahedron is reflected or not.

The transformation from one card to another is an isometry of the octahedron. In the above example, the rotation is 90° clockwise around the line that goes from the top vertex to the bottom vertex. So from the first card to the second card, the purple and green rotate one space over, and the pink rotates behind the octahedron where the orange used to be, which is rotated into view. The rotation from the second card to the third card is the same.

Note that the isometry of the octahedron is the same as the isometry of the cube -- this is not a coincidence.
The bottom half of each card depicts an arrangement of three colors with some "holes" attached. The transformation from one card to another is a permutation of the positions, followed by toggling the holes in any number of positions.

In the above example, to go from one card to the next, you swap the bottom two positions and toggle the hole in the bottom right position.
The top half of each card depicts an arrangement of four colors plus a swirl, which is either black or white. The transformation from one card to another is a permutation of the positions, plus optionally flipping the swirl.

In the above example, to go from one card to the next, you move top-left to bottom, bottom to top-right, top-right to center, and center to top-left; and you do not flip the swirl.

Again, all four characterizations are equivalent, so you can find all sets by ignoring the cube and only looking at the octahedron or vice versa. Mathematically,

The first corresponds to the isometry group of the cube.
The second corresponds to the isometry group of the octahedron.
The third corresponds to the abstract group C₂≀S₃. (This is a wreath product.)
The fourth corresponds to the abstract group S₄×C₂.

All four groups are isomorphic to the octahedral group, whence the name.

A5SET

difficulty: medium

cards: 60 (deal 10)

pronounced "asset"

Here is an example of a set in A5SET:

A5SET is very similar to OCTA; you should read those rules if you haven't already.

Now that you've read the rules to OCTA, you know what I'm about to say: a set is three cards where the operation from the first to the second is the same as the operation from the second to the third, and there are four equivalent ways to think of this:

The top half of each card depicts a dodecahedron (12-sided polyhedron). The transformation from one card to another is a rotation of the dodecahedron.
The bottom half of each card depicts an icosahedron (20-sided polyhedron). The transformation from one card to another is a rotation of the icosahedron.

Here is a sketch of the rotation represented in the example above; notice how the colors follow the arrows:
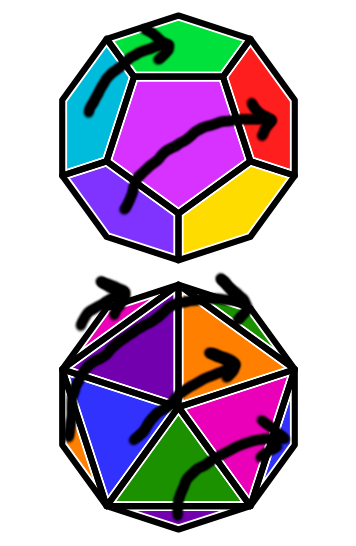
The top half of each card depicts a subset of the arrangements of 6 colors. The transformation from one card to another is a permutation of the positions.
The bottom half of each card depicts a subset of the arrangements of 5 colors. The transformation from one card to another is a permutation of the positions.

(You can ignore the tiny triangles on the outsides; they are fully determined by the triangles that are actually visible.)

And mathematically,

The first corresponds to the symmetry group of the dodecahedron.
The second corresponds to the symmetry group of the icosahedron.
The third corresponds to a particular embedding of A₅ in A₆.
The fourth corresponds to the abstract group A₅.

All four groups are isomorphic to the alternating group A₅, whence the name.

There is a very useful lemma for finding sets in A5SET; to demonstrate it, here is another example of a set in A5SET:

You will notice that in the first example, the bottom right face of the dodecahedron is yellow in all of the cards; and in the second example, the bottom left and top right faces of the icosahedron are the same in all cards. In fact, there are only two classes of rotations that can form sets in A5SET:

Rotations that fix exactly once dodecahedron face color, like the first example. (These correspond to order 5 group elements.)
Rotations that fix exactly two icosahedron face colors, like the second example. (These correspond to order 3 group elements.)

Furthermore, all rotations that fit the above conditions form sets; for example, if you find three cards where one of the dodecahedron faces is the same in all cards and all other dodecahedron faces are different in all cards, you can be sure it's a set.

S3CT

difficulty: very hard

cards: 72 (deal 10)

pronounced "sect"

Here is an example of a set in S3CT:

Like in OCTA, a set in S3CT is three cards where the way to go from the first card to the second card is the same as the way to go from the second card to the third card.

In the above example, to go from the first card to the second card, you grab the bottom triangle, move it to the top, and rotate it clockwise a little. From the second card to the third card, you also move the bottom triangle up and slightly clockwise. Similarly, between both pairs, the top triangle is moved down, reflected across a vertical line, and rotated counterclockwise a little.

The underlying mathematical object is the natural torsor for the wreath product S₃≀C₂, whence the name.

S3CT is perhaps the variant with the most dramatic contrast between difficulty after first learning the rules and difficulty after learning some strategies. In particular, it becomes much easier when you consider two cards as the first and third elements of a set (the "ends"), and look for the card in the middle. To do this quickly, it is very helpful to categorize cards by parity.

Each card has two kinds of parity -- essentially, ways of splitting the deck into two groups. The first one is whether the black or gray spiral is on top, which I'll call translational parity. The second one is whether the two spirals go in the same direction, which I'll call rotational parity. A crucial fact for finding sets is: if two cards are the ends of a set, both parities must be the same. (The reason is that the operation between two cards either flips parity or doesn't; and since you're applying it twice, you either don't change the parity or change it and then change it back.)

Now that we've labelled the cards like this, we can categorize all the different kinds of sets. The first thing to look at is whether the spirals change directions between the two end cards. (Remember that since rotational parity is fixed, either both do or neither do.)

If the spirals don't change direction, the middle card must have the same rotational parity as the ends. We can then further categorize these sets by what happens in each triangle between the ends:
- If one of them rotates and one of them stays the same, the middle card must have the same translational parity as the ends, it has to have the third rotation of the rotating triangle, and the other triangle has to share at least one dot with the ends (in other words, it's either still the same or one of the three reflections).
- If both of them rotate in the same direction,
- If both of them rotate in opposite directions,
If the spirals do change direction, the situation is a lot simpler. First, note that there is exactly one dot that stays in the same place in each triangle. The set above is an example of this: the red dot stays fixed in the black triangle, and the green dot stays fixed in the gray triangle.

Now, the middle card must have the opposite translational and rotational parity. And such a card completes the set if and only if the fixed dots swap places. In the above example, note that in the middle card, the green dot takes the place of the red dot, and vice versa.

C3C3

difficulty: ???

cards: 81 (deal 12)

pronounced "kee-kee"

Here is an example of a set in C3C3:

Credits / About

These variants were inspired in part by Nonabelian Set by Cathy Hsu, Jonah Ostroff, and Lucas Van Meter. (In fact, octaset is based on the same group, but uses a torsor instead.)

Many ET people contributed to creating these variants; these include Alex Bean, Andy Tockman (who made this website), Della Hendrickson (who printed the physical decks), Josh Brunner, Joshua Ani, and Yan Sheng Ang.

The code that runs this website is open source, licensed under GPLv3. The backend is Haskell, and the frontend is plain JavaScript.

If you have any questions, comments, suggestions, etc, you can contact me.